Introdução

A matemática atuarial pode se beneficiar convenientemente da notação vetorial. Isso é possível por várias razões. Por exemplo, o Valor Presente Atuarial – VPA é um operador linear equivalente ao produto escalar entre dois vetores. Entre as muitas vantagens possíveis, obter uma notação atuarial que facilite a programação dos cálculos é altamente vantajoso tanto pela clareza quanto pela eficiência.

Considere dois vetores $\textbf{v} = (v_1,\dots,v_n)$ e $\textbf{w} = (w_1,\dots,w_n)$ ambos com o mesmo número de coordenadas. Definimos o produto Hadamard, ou produto ponto a ponto entre $\textbf{v}$ e $\textbf{w}$ como $$\textbf{v}\odot\textbf{w} = (v_1w_1,\dots,v_nw_n).$$ Isto é, o produto Hadamard entre vetores é uma operação binária que toma dos vetores e os transforma em um terceiro vetor cujas coordenadas são o produto de cada par de coordenadas dos vetores do domínio. Ou seja, $\odot:\mathbb{R}^n\times\mathbb{R}^n\rightarrow\mathbb{R}^n$.

Valor Presente Atuarial

O VPA é valor esperado de um fluxo de caixa descontado. Calcular o VPA equivale a avaliar um fluxo de caixa em uma data focal, ponderando cada fluxo por uma probabilidade de sobrevivência. Seja $v^n$ o fator de desconto financeiro, ${_n}p_x$ as probabilidades de sobrevivência e $c_n$ o fluxo financeiro propriamente dito, então o VPA é definido como $$VPA_x = \sum_{n=1}^{\infty}v^n{_n}p_xc_n.$$ Ele calcula o valor presente de um fluxo de pagamentos $c$ pagos de forma postecipada ao longo da vida de uma pessoa de idade $x$. Por exemplo, definindo $c_n = 1$ para todo $n$.

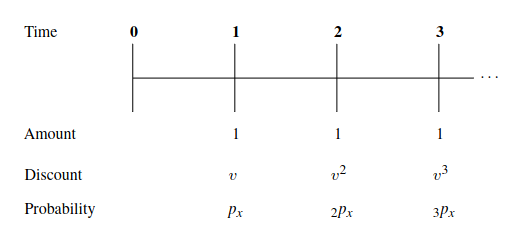
Considerando o diagrama, o VPA calculado seria $vp_x+v^2{_x}p_x+v^3{_3}p_x+\cdots$. Há muitas possibilidades para arranjos de cálculos, como antecipação, diferimento, prazo fixado, com valores de fluxos contantes, crescentes e assim por diante. Entretanto, para os objetivos desse texto, basta a definição básica.

Fluxos Atuariais

Em muitas ocasiões, sobretudo ao desenvolvermos sistemas para implementar modelos atuariais, a estratégia mais viável é operar no fluxo atuarial diretamente, ao invés de calcular o valor presente. Afinal, uma vez que tenhamos calculado os fluxos, fica fácil obter o valor presente. Inclusive, ao elaborarmos uma avaliação atuarial, os fluxos atuariais são parte integrante do relatório final.

Podemos definir o fluxo atuarial de várias maneiras, mas a legislação brasileira aplicada aos Regimes Próprios de Previdência Social afirma que:

Os fluxos atuariais são a discriminação dos fluxos de recursos, direitos, receitas e encargos do plano de benefícios do RPPS, benefício a benefício, período a período, que se trazidos a valor presente pela taxa atuarial de juros adotada no plano, convergem para os resultados do Valor Atual dos Benefícios Futuros e do Valor Atual das Contribuições Futuras que deram origem aos montantes dos fundos de natureza atuarial, às provisões matemáticas (reservas) a contabilizar e ao eventual deficit ou superavit apurados da avaliação atuarial.

Observando mais uma vez a figura do fluxo, essa definição implica que o fluxo atuarial deve incorporar a probabilidade de sobrevivência, portanto, em sua forma temporal, é um fluxo ponderado por tais probabilidades. Outra parte importante da definição implica que ao descontarmos esse fluxo pela taxa de desconto atuarial, ele deve convergir para o valor atual da contribuições futuras (receitas) e dos benefícios futuros (despesas). Se simplificarmos ao essencial, vemos que:

Os fluxos atuariais são fluxos de recursos, direitos, receitas e encargos (…) que se trazidos a valor presente pela taxa atuarial de juros adotada no plano, convergem para seus respectivos valores atuais (…).

Considerando isso, temos que o fluxo atuarial consiste nos termos $v^n{_n}p_x$ na definição do VPA. Veremos agora como a notação vetorial é útil para modelarmos os fluxos.

Fluxos Atuariais e a Notação Vetorial

Seja $\omega$ a idade limite em uma tábua atuarial, isto é, a idade máxima que um indivíduo poderá atingir e seja $x$ a idade do indivíduo em relação ao qual estamos calculando o VPA. Sejam $\textbf{v} = (v^1,\dots,v^{\omega-x})$ um vetor contendo os fatores de descontos a serem aplicados em cada fluxo e seja $\textbf{c} = (c_1,\dots,c_{\omega-x})$. Além disso, seja $\textbf{p} = (p_x,\cdots,{_{\omega-x}}p_x)$ o vetor contendo as probabilidades de sobrevivência. Por fim, seja $\textbf{1}$ um vetor cujas coordenadas são iguais a $1$ e que tem o mesmo número de coordenadas que os demais vetores e considere $\langle\cdot,\cdot\rangle$ o produto escalar de vetores.

Considerando a definição do produto Hadamard, definimos $$\textbf{f}_x = \textbf{p}\odot\textbf{c} = (p_xc,\dots,{_{\omega-x}}p_xc_{\omega-x}).$$ Observe que $\textbf{f}_x$ é, precisamente, o fluxo atuarial relativo aos benefícios em $\textbf{c}$. A partir disso, utilizando o produto escalar e $\textbf{v}$, podemos obter o APV como $$APV_x = \langle\textbf{1},\textbf{f}_x\odot\textbf{v}\rangle, $$ onde $\textbf{f}_x\odot\textbf{v} = (vp_xc,\dots v{_{\omega-x}}p_xc_{\omega-x})$.

Ao fim do dia, estamos falando da mesma coisa, em uma notação diferente, qual a vantagem disso? Pois bem, a clareza. Se considerarmos apenas o VPA, não parece grande coisa, mas conforme as metodologias ganham complexidade, ao incluirmos definições de benefício, vidas conjuntas, reversão de pensão e outros fatores, as formulações ganham complexidade e se tornam menos óbvias. Além disso, fica mais fácil programar o cálculo em uma linguagem vetorizada, como o R, quando nossas funções já estão definidas em função de vetores.

É simples programar esse cálculo na linguagem R, por exemplo. Bastaria definirmos o vetor $\textbf{v}$ com cada coordenada igual ao fator de desconto $v$ e utilizando a função cumprod para gerar um novo vetor com cada coordenada $j$ igual à $v^j$. Além disso, lembrando que ${_n}p_x = \prod_{k=0}^{n-1}p_{x+k}$, podemos com a mesma função cumprod gerar o vetor com probabilidades de sobrevivência. Tomando o vetor de fluxos, bastaria fazer o produto dos vetores resultantes e depois somá-los e teríamos o APV. Note que o calculo é feito de forma vetorizada, dispensando a necessidade de loops. Verifique aqui uma implementação.

Conclusões

Nesse breve texto apresentamos o produto Hadamard de vetores, bem como a definição de valor presente atuarial. Também vimos a definição de fluxos atuariais. Além disso, discutimos como o uso da notação vetorial pode ser útil para simplificar a definição matemática de fluxo atuarial e do valor presenta atuarial, discutindo suas vantagens. Por fim, vimos como é fácil programar o cálculo em uma linguagem vetorizada, quando sua formulação é também baseada em notação vetorial.