Introdução

Em qualquer cálculo onde não dispomos de informação completa, precisamos fazer suposições sobre quantidades desconhecidas. Na avaliação atuarial, as hipóteses atuariais são um conjunto de suposições que, juntamente com os dados, quando introduzidas em um modelo atuarial, permitem a execução dos cálculos no modelo.

Um modelo atuarial simplificado

Para ilustrar como hipóteses atuariais são aplicadas em cálculos, veremos um modelo simplificado que estima o custo normal anual de um benefício de aposentadoria. Suponha que o valor da contribuição normal que o patrocinador deve pagar em relação a um funcionário é determinado pela idade atual $x$ e pela idade de ingresso no $y$, de acordo com a seguinte equação quadrática: $$C(x) = \alpha (x-y)^2+\beta (x-y) +\gamma$$Nesta equação, $C(x)$ representa o custo normal atribuído ao funcionário de idade $x$. Caso tivéssemos todas as informações necessárias, bastaria substituir o valor de $x$ e encontraríamos o valor da contribuição. No entanto, para resolver essa equação precisamos de $x,y,\alpha, \beta$ e $\gamma$. Nesse caso, $x\text{ e } y$ são valores que obtemos dos dados disponíveis, enquanto os coeficientes da equação, não. Logo, precisamos fazer algumas suposições acerca desses coeficientes.

Suposições para os parâmetros

Agora, detalharemos as suposições necessárias para determinar os coeficientes $\gamma$, $\beta$ e $\alpha$, bem como sua relação com o contexto do modelo. Considerando o exemplo apresentado, vamos analisá-lo um pouco mais de perto. Sabemos que $x\geq0$, pois representa a idade atual do funcionário. Quando $x=y$, ou seja, no ano em que o funcionário é contratado, o valor da primeira contribuição será uma constante $\gamma$. Suponha que o salário anual inicial do funcionário seja $S_0 = 100000$ e que $\gamma = 0.11S_0 = 11000$. Ou seja, $\gamma$ é uma proporção fixa do primeiro salário anual. Admita que somente o empregador arca com a contribuição total.

Para cada ano de serviço, a contribuição do patrocinador sofrerá um incremento linear de $\beta = 20$, como um estímulo à permanência do funcionário nos quadros da empresa. Mas não basta permanecer na empresa, o funcionário precisa cumprir um programa de educação continuada ao longo de sua carreira, cumprindo algumas horas de cursos técnicos todo ano. Digamos que a meta de horas de educação continuada ao longo de um ano seja de $h = 200$ e seja $h_x\leq200$ a quantidade de horas de cursos cumpridas pelo funcionário. Como forma de incentivar o cumprimento das horas de estudos, ficou definido que $\alpha = e^{-(200-h_x)}$. Sendo assim, sabendo que o funcionário contava com $20$ anos de idade quando foi contratado, o modelo final é o seguinte: $$C(x) = e^{-(200-h_x)}(x-20)^2+20(x-20)+11000$$
Observe que o coeficiente $\alpha$, na forma como o definimos, reflete o impacto do cumprimento (ou não) da meta anual de 200 horas de educação continuada. Quanto menor o número de horas cumpridas ($h_x$), menor será o valor de $\alpha$, o que reduz, exponencialmente, o incentivo a longo prazo. Além disso, embora no exemplo tenhamos feito suposições baseadas em critérios racionais sobre $\gamma$, $\beta$ e $\alpha$, na prática, podemos estimar esses parâmetros usando ferramentas estatísticas ou dados históricos.

Implementação computacional em R

Com isso, podemos calcular o custo normal para um funcionário com $x$ anos de idade, contratado aos $20$ anos com um salário anual inicial de cem mil reais e que precisa cumprir até $200$ horas de educação continuada por ano. O código é o seguinte:

custo <- function(idade, horas){
  retorno <- exp(-(200-horas)) * (idade-20)^2 + 20 * (idade-20) + 11000
  return(retorno)
}
idade <- seq(20, 50, 1)
par(mfrow=c(2,2))
plot(idade, custo(idade, 200), type = "l", xlab = "Idade", ylab = "Custo Normal")
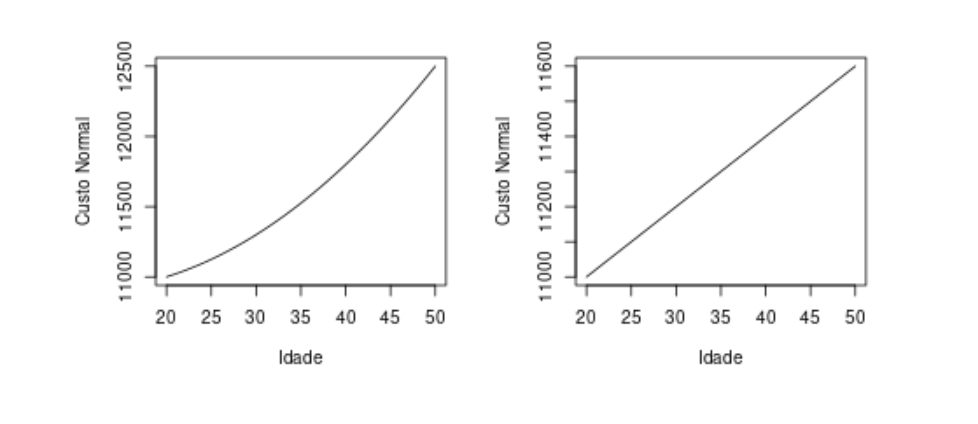
plot(idade, custo(idade, 80), type = "l", xlab = "Idade", ylab = "Custo Normal")

Os gráficos abaixo mostram a variação do custo normal com a idade do funcionário para dois cenários distintos de cumprimento de horas de educação continuada: (1) cumprimento total das 200 horas anuais e (2) apenas 80 horas cumpridas.

Considerações finais

Vimos ao longo do texto como as hipóteses atuariais são indispensáveis para a execução do cálculo atuarial. Enquanto os dados fornecem a base para o modelo, os parâmetros frequentemente dependem de suposições construídas com base em características da população, contexto econômico e outros fatores. Pequenas variações nessas hipóteses podem gerar impactos significativos nos resultados, o que torna a validação e a análise de sensibilidade etapas fundamentais para aumentar a confiabilidade do cálculo.

Este exemplo reforça que a construção de hipóteses atuariais exige não apenas uma base teórica sólida, mas também uma compreensão profunda do contexto econômico, social e organizacional em que o modelo será aplicado. Essa abordagem integrada é necessária para produzir cálculos robustos e alinhados às necessidades práticas.

Em relação ao modelo apresentado, há diversas formas de torná-lo mais realista. Poderíamos, por exemplo, definir $\gamma$ como uma função do salário ao longo do tempo, permitindo que ele varie conforme o funcionário progride na carreira. Poderíamos também ajustar $\beta$ de acordo com a quantidade de horas de estudo cumpridas ou mesmo incluir um bônus extra para funcionários que excedam a meta de horas. Essas alterações demonstram a flexibilidade dos modelos atuariais e como ajustes cuidadosos podem refletir melhor as particularidades de cada caso.

Investir na melhoria contínua e no alinhamento das hipóteses com a realidade é indispensável para garantir que os cálculos atuariais sejam não apenas precisos, mas também relevantes e aplicáveis ao cenário em análise.